Main Works
A collection of highly interesting projects I contributed to.
In this page :
Learning Self-Supervised Dynamic Networks for Seizure Analysis
Mar 8, 2024
- Self-supervised learning
- multivariate time series
- graph neural networks
- seizure analysis

Recurrent Graph Neural Networks are very effective at modeling brain activity, thanks to their spatial-temporal inductive bias, and they show further capabilities when we apply self-supervised pretraining methods. For instance, they show improved performances on epileptic-seizure analysis, namely detection and classification, compared to convolutional and classical recurrent neural networks. Still, the graphs used by these methods are generally predefined, and often provide little insight on the task.
In this paper, presented at ICLR 2024 Workshop on Learning from Time Series For Health, we build upon current advancements in graph learning for time series forecasting to propose a novel architecture to learn task-specific networks, jointly with a self-supervised pretraining strategy. We study the performances of learned graphs at different scale, by comparing static and dynamic networks, and illustrate the outstanding performance of our model on epilepsy classification and detection tasks.
Byzantine-robust decentralized optimization for Machine Learning
Feb 4, 2021
- Master thesis
- Stochastic Gradient Descent
- Decentralized optimization
- Machine Learning
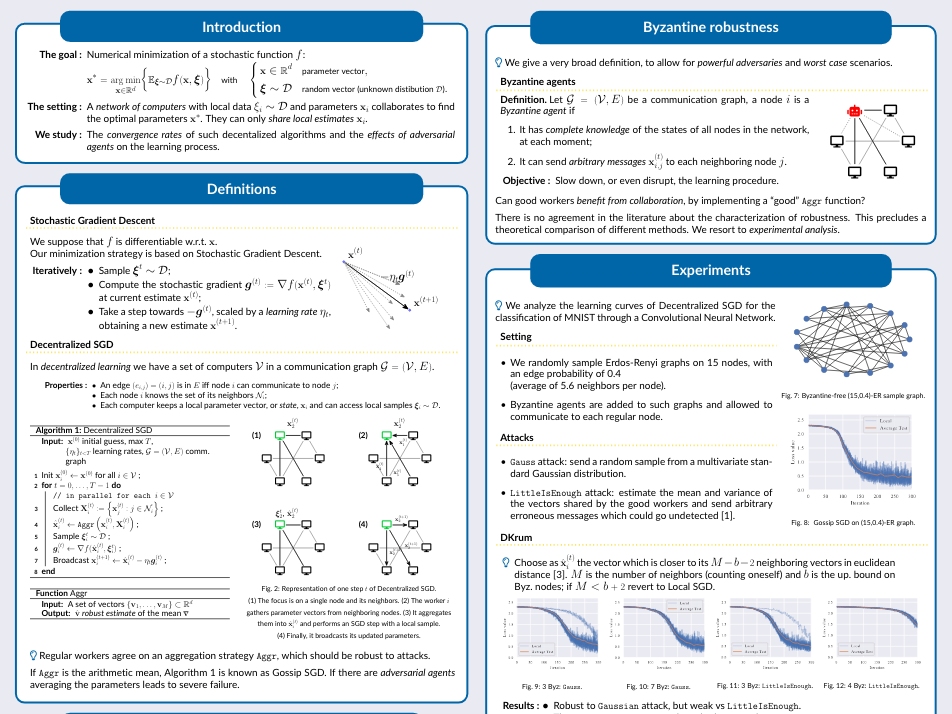
This essay analyses a Byzantine-resilient variant of Decentralized Stochastic Gradient Descent.
We motivate and define the decentralized Stochastic Gradient Descent algorithm, in which a network of computers aim to jointly minimize a parametrized stochastic function. Then, we introduce Byzantine adversaries, whose goal is to impair the the optimization process by sending arbitrary messages to regular workers.
We review many variants of the decentralized SGD algorithm, which have been designed to withstand such Byzantine attacks. We present their assumptions and discuss their limitations.
We carry on a general theoretical analysis on the behavior of Robust Decentralized SGD, by providing convergence rates for a Byzantine-free setting. We prove sublinear convergence in the number of iterations T, and a dependence on the number of good nodes N and on the connectivity of the graph, represented by the spectral gap \(\rho\).
We perform a series of experiments on the MNIST handwritten-digit classification task. We test different communication networks and variants of Robust DeSGD against two different kind of Byzantine attacks.
Finally, we point out the lack of a univocal definition of Byzantine-robustness, and the consequent confusion on the meaning of failure in a this setting. We propose a convergence based approach, which discuss the performance by comparing it to the learning rate of local SGD, which is always a solution for the iid setting that we consider.
Polyadic Quantum Classifier
Jul 28, 2020
- quantum machine learning
- variational quantum algorithm
- NISQ architecture
- classification algorithm
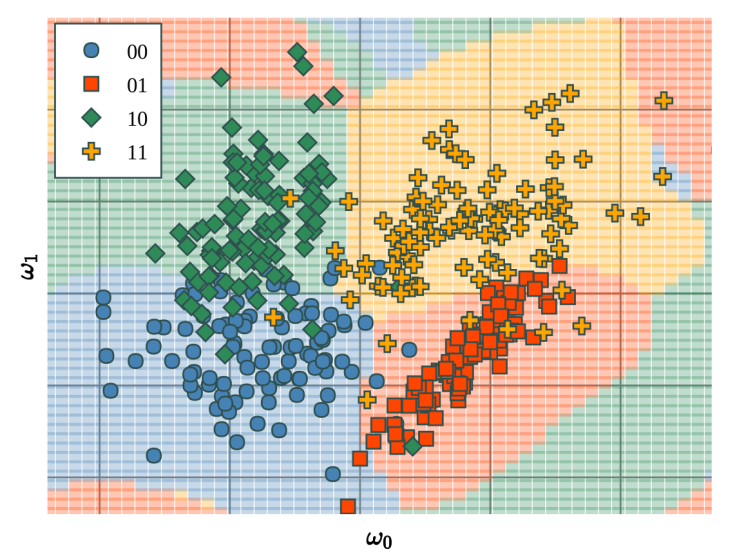
In this paper, we introduced a supervised quantum machine learning algorithm for multi-class classification on Noisy Intermediate-Scale Quantum computers. With this procedure, we have been able to fully train a model on a real quantum computer, for the first time in the field. The model managed to classify the Iris Flower dataset with the same accuracy as a classical model. You can explore the dataset and the training process at https://iris.entropicalabs.io.
In the paper, to be published at the QCE20 inetrnational conference, we discuss other experiments, along with the insight we gained in designing quantum circuits for the classification task.
The source code of the experiment evolved in the polyadicQML python library, which implements an interface to train and deploy machine learning models using quantum coputers, and quantum simulators.
Polyadic QML package
Jul 23, 2020
- Python package
- quantum machine learning
- variational quantum algorithm
- classification algorithm

This package provides an high level API to define, train and deploy Polyadic Quantum Machine Learning models. It implements a general interface which can be used with any quantum provider. As for now, it supports a fast simulator, manyq, and Qiskit. More are coming.
With polyadicQML, available on PyPI, training a model on a simulator and testing it on a real
quantum computer can be done in just a few lines, with an interface very familiar to any sklearn user.
I developped this project while working at Entropica Labs, a Quantum-Software start-up based in Singapore and we used the package to train and test classifiaction models on actual quantum computers, as described in the Poliadic Quantum Classifier paper, presented at the QCE20 international conference.
Convolutional Neural Tangent Kernel
Jan 11, 2019
- Neural Tangent Kernel
- Artificial Neural Networks
- Convolutional Networks
- Kernel regression
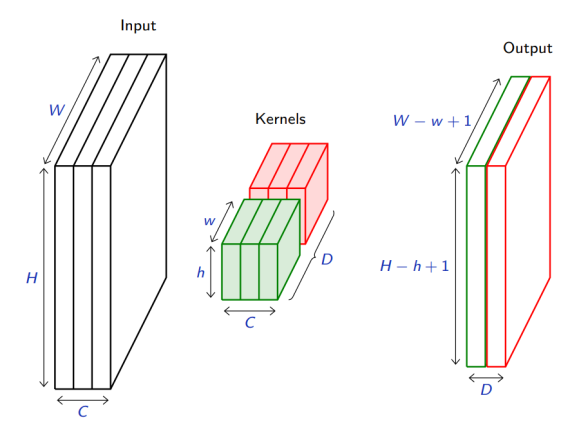
In this paper, I study the relation between artificial neural networks and kernel regression. I start by defining some neural networks, such as the multilayer perceptron (MLP) and the convolutional neural network (CNN); then I discuss some theoretical results that support the equivalence with kernel methods. I use \emph{tensor programs} to see that at initialization infinitely wide neural networks are equivalent to Gaussian processes. Then, I study the \emph{Neural Tangent Kernel}, which gives the direction along which the network evolves during training. In the infinite width limit of MLPs, this kernel converges to a finite one and is constant during training. Furthermore, if the MLP is big enough, with high probability, the function given by the network after training is close to the function given by the kernel regressor using the limiting Neural Tangent Kernel.
At this point, I test the kernel regressor against the actual neural network. I do so with a multilayer perceptron and a convolutional neural network, which I train and test on the MNIST handwritten digits dataset, on a classification task.
I produced this report for a semester project under the supervision of Professor C. Hongler and Dr. F. Gabriel, during my MSc in Applied Mathemetics at EPFL.