William Cappelletti

Analysis of litter on Swiss shores

Jun 19, 2019

• Statistics
• Generalized Linear Models
• Generalized Additive Models
• Data analysis

• Read it

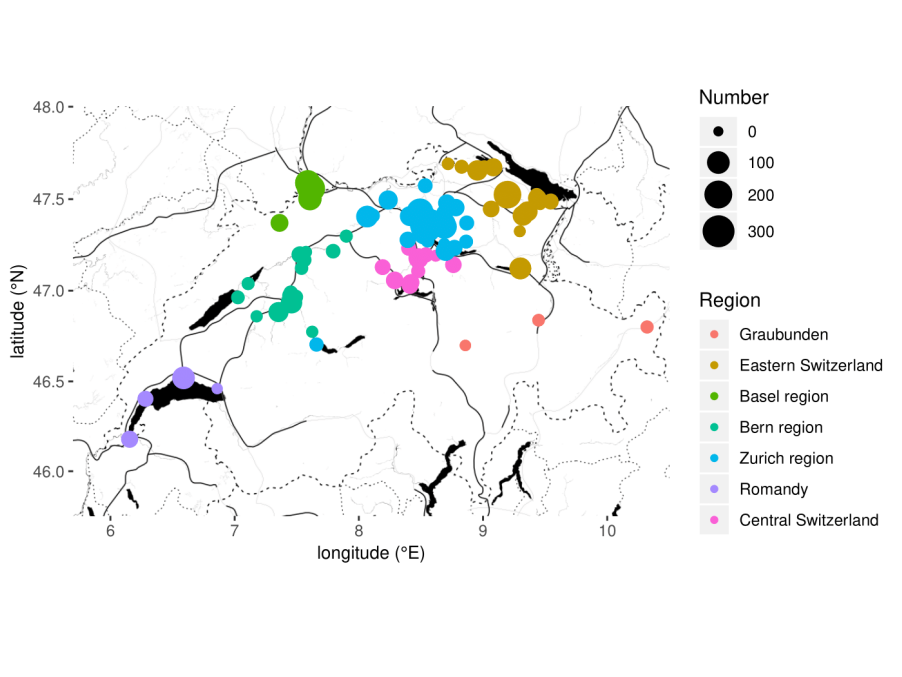
We analyze a data set on cigarette butts count on different shores in Switzerland.

We fit three different Generalized Linear Models and a Generalized Additive Model with Negative Binomial distribution using various geographical and temporal information. Then, we extensively discuss our final model, observing an interesting seasonal effect and some regional peculiarities.

Finally, we use our results to give confidence intervals for the cigarette butts count in the month of August 2019 for all the considered beaches, with a particular attention to those on the shores of Geneva Lake. We regress their expected mean by smoothing on both the months and the inverse of the length of the beach, accounting for a fixed effect given by the Region and a random effect from the beach.

Crowded enzyme kinetics using simulation and machine learning

Dec 13, 2018

• Machine Learning for science
• Gradient Boosting
• Computational Chemistry

• Read it

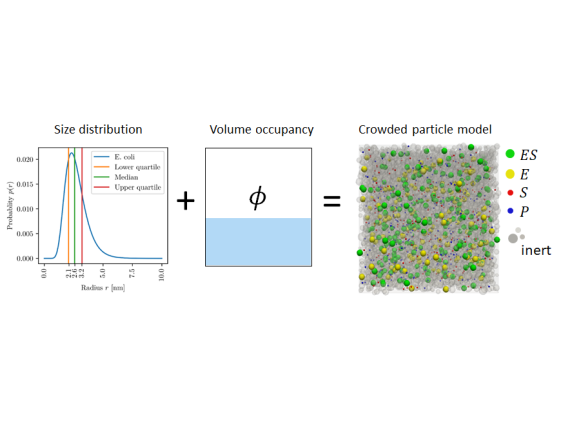
We derive a model to predict the four kinetic rate constants of the reversible Michaelis-Menten enzymatic reaction mechanism in a crowded environment. The model is trained on simulated data obtained from a crowded particle model which has the following features: reactant concentrations, volume exclusion fraction and mass distribution of inert particles.

Reproducing the previous work done on the available dataset, we first perform weighted linear regressions for each combination of volume exclusion and mass distribution parameters which is our baseline model. We then implement several machine learning algorithms and develop a generalized model integrating all the parameters.

Our final model makes use of the computationally efficient gradient boosting algorithm XGBoost and is composed by four boosters, each one trained to predict one of the kinetic rate constants. This model significantly increases the prediction power compared to the previous aforementioned baseline model.

On the volume of zonotopes

Jun 8, 2018

• Convex Geometry
• Zonotopes
• Projections
• Volume maximization

• Read it

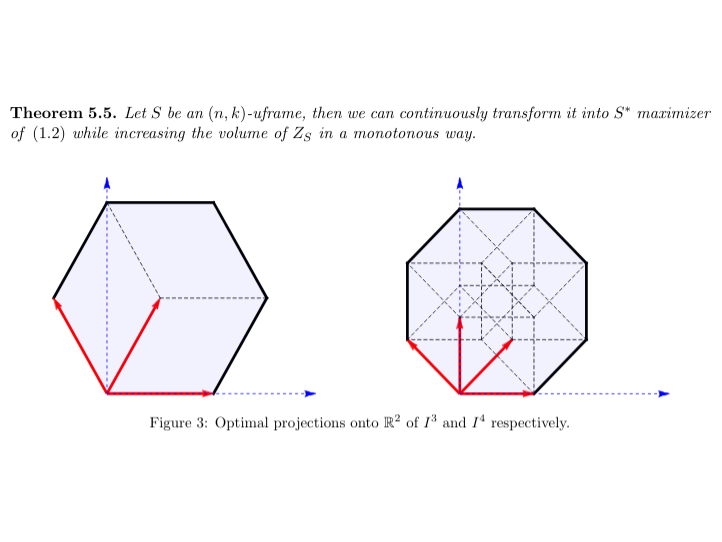
I study properties of a projection of an hypercube \(I^n = [0,1]^n\) onto a k-dimensional subspace. This projection can be seen as a zonotope in \(\mathbb{R}^k\), which is the Minkowski sum of linear segments. Studying particular transformations and small perturbations of a projection, I find necessary conditions for it to have the maximal volume. Finally, I give a new approach to find the optimal upper bound on the volume of a projection onto a two-dimensional subspace.

This is the final Project for my BSc in Mathematics at EPFL, which I carried on under the supervision of Professor J. Pach and Dr. G. Ivanov.